Re: cost_sort() improvements
| From: | Teodor Sigaev <teodor(at)sigaev(dot)ru> |
|---|---|
| To: | Pgsql Hackers <pgsql-hackers(at)postgresql(dot)org> |
| Subject: | Re: cost_sort() improvements |
| Date: | 2018-07-12 14:31:58 |
| Message-ID: | ee14392b-d753-10ce-f5ed-7b2f7e277512@sigaev.ru |
| Views: | Whole Thread | Raw Message | Download mbox | Resend email |
| Thread: | |
| Lists: | pgsql-hackers |
> At least [1] and [2] hit into to that issues and have an objections/questions
> about correctness of cost sort estimation. Suggested patch tries to improve
> current estimation and solve that issues.
Sorry for long delay but issue was even more complicated than I thought. When I
tried to add cost_sort to GROUP BY patch I found it isn't work well as I hoped
:(. The root of problem is suggested cost_sort improvement doesn't take into
account uniqueness of first column and it's cost always the same. I tried to
make experiments with all the same and all unique column and found that
execution time could be significantly differ (up to 3 times on 1e7 randomly
generated integer values). And I went to read book and papers.
So, I suggest new algorithm based on ideas in [3], [4]. In term of that papers,
let I use designations from previous my email and Xi - number of tuples with
key Ki, then estimation is:
log(N! / (X1! * X2! * ..)) ~ sum(Xi * log(N/Xi))
In our case all Xi are the same because now we don't have an estimation of
group sizes, we have only estimation of number of groups. In this case,
formula becomes: N * log(NumberOfGroups). Next, to support correct estimation
of multicolumn sort we need separately compute each column, so, let k is a
column number, Gk - number of groups defined by k columns:
N * sum( FCk * log(Gk) )
and FCk is a sum(Cj) over k columns. Gk+1 is defined as estimate_num_groups(NGk)
- i.e. it's recursive, that's means that comparison of k-th columns includes all
comparison j-th columns < k.
Next, I found that this formula gives significant underestimate with N < 1e4 and
using [5] (See Chapter 8.2 and Theorem 4.1) found that we can use N + N * log(N)
formula which actually adds a multiplier in simple case but it's unclear for me
how to add that multimplier to multicolumn formula, so I added just a separate
term proportional to N.
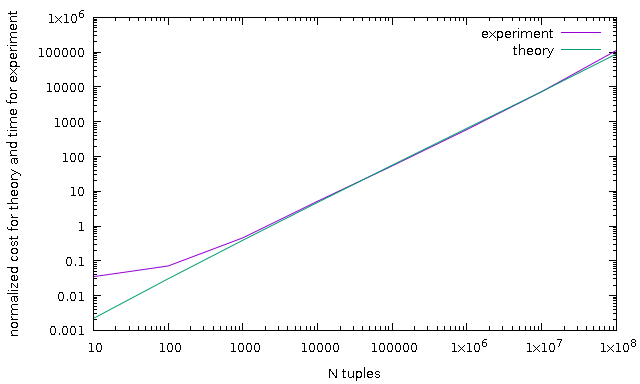
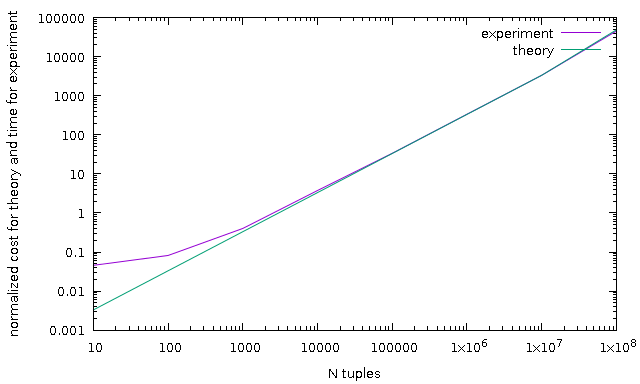
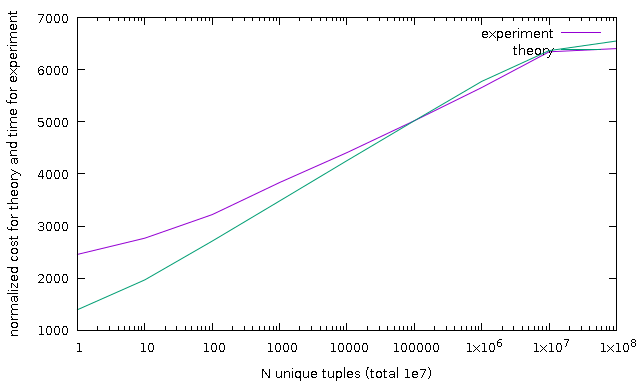
As demonstration, I add result of some test, *sh and *plt are scripts to
reproduce results. Note, all charts are normalized because computed cost as not
a milliseconds. p.pl is a parser for JSON format of explain analyze.
N test - sort unique values with different number of tuples
NN test - same as previous one but sort of single value (all the same values)
U test - fixed number of total values (1e7) but differ number of unique values
Hope, new estimation much more close to real sort timing. New estimation
function gives close result to old estimation function on trivial examples, but
~10% more expensive, and three of regression tests aren't passed, will look
closer later. Patch doesn't include regression test changes.
> [1] https://commitfest.postgresql.org/18/1124/
> [2] https://commitfest.postgresql.org/18/1651/
[3] https://algs4.cs.princeton.edu/home/, course Algorithms,
Robert Sedgewick, Kevin Wayne,
[4] "Quicksort Is Optimal For Many Equal Keys", Sebastian Wild,
arXiv:1608.04906v4 [cs.DS] 1 Nov 2017
[5] "Introduction to algorithms", Thomas H. Cormen, Charles E.
Leiserson, Ronald L. Rivest, ISBN 0-07-013143-0
--
Teodor Sigaev E-mail: teodor(at)sigaev(dot)ru
WWW: http://www.sigaev.ru/
| Attachment | Content-Type | Size |
|---|---|---|
| cost_sort-v7.patch | text/x-patch | 10.8 KB |
| p.pl | application/x-perl | 614 bytes |
|
image/png | 13.2 KB |
| N.plt | text/plain | 226 bytes |
| N.sh | application/x-shellscript | 338 bytes |
|
image/png | 13.0 KB |
| NN.plt | text/plain | 227 bytes |
| NN.sh | application/x-shellscript | 342 bytes |
|
image/png | 14.1 KB |
| U.plt | text/plain | 230 bytes |
| U.sh | application/x-shellscript | 340 bytes |
In response to
- cost_sort() improvements at 2018-06-28 16:47:22 from Teodor Sigaev
Responses
- Re: cost_sort() improvements at 2018-07-12 14:48:21 from Teodor Sigaev
- Re: cost_sort() improvements at 2018-07-22 20:22:10 from Tomas Vondra
Browse pgsql-hackers by date
| From | Date | Subject | |
|---|---|---|---|
| Next Message | Andrew Dunstan | 2018-07-12 14:33:53 | Re: _isnan() on Windows |
| Previous Message | Tom Lane | 2018-07-12 14:20:22 | Re: _isnan() on Windows |